Maya Tool - Expression Parser - Part 1
- Dominik Haase

- Oct 10, 2023
- 10 min read
Updated: Oct 18, 2023
When I started this project, I had no idea what I was getting myself into! Throughout the years, I built various systems to simplify the creation of node graphs in Maya. Inspired by my previous experiments with my Maya point wrangle node and annoyed by the extra code I had to type in my latest approach, I wanted to create something better...
aim = v@target.translate - v@main.translate
up_fake = v@up.translate - v@main.translate
side = aim ^ up_fake
up = side ^ aimGenerating Node networks from expressions is not a new idea. There are several tools like Chad Vernon's Dependency Graph Expressions (DGE) or Serguei Kalentchouk's Maya Math Nodes. There was also one that I can't remember the name of, that implemented custom types directly in Python. (If you know the one I mean, let me know and I will link it here!)
...but I wanted to create my own :)
A disclaimer before diving deeper into this, this is not a tutorial, and everything you read here, including the terminology I use, should be taken with a big grain of salt as I have (as usual) no idea what I am actually doing... Nevertheless, reach out with any questions and I'll do my best to help :) Or, let me know if you notice anything wrong!!
The First
As mentioned above, this has been a lengthy project so far and probably will be for a little longer. However, the first test was pretty quick thanks to this post by Don Cross (unfortunately it is no longer available for free though his GitHub project still is). There are enough posts about lexers and parsers out there by people who are far more qualified than me so I leave it up to you to look that up or not. Don's post is about a simple expression parser and I'll give you a quick insight into my implementation.
First, identifying tokens. This is pretty straightforward using regex. These are far from all the patterns I implemented, but they give a good reference point.
(you will notice some variable names got abbreviated and some lines compressed, this is so I can fit everything into a single line of the code box, don't do this in your code!)
class Operator:
SIGN = r"(?:[+-]{0,1})"
ADD = r"(?:[+-]{1})"
MULTIPLY = r"(?:[\*/]{1})"
POWER = r"(?:\^)"
ASSIGN = r"(?:=)"
COMPARE = r"(?:==|!=|<=|>=|<|>)"
LOGIC = r"(?:&&|\|\|)"
# any is just any of the above (shortened for line length reasons)
OPERATOR = r"(?:&&|\|\||==|>=|<=| ... |\/|\*|\^|,|\[|\]|=|\n|;)"
NUMERIC = r"(?:[0-9]+(?:\.[0-9]+){0,1})"
VARIABLE = r"(?:[A-Za-z_][A-Za-z_0-9]*)"
FUNCTION = rf"(?:{VARIABLE}\(.*\))"
VECTOR = r"(?:\[.+\])" # validate whats inbetween [ and ] later
VECTOR_ACCESS = rf"(?:{VARIABLE}\[\d+\])"
# while this first implementation was generally untyped, the tool adds
# missing attributes on nodes. For that, it needs to know the type
# furthermore, in some cases, the exact type cannot be determined by
# the plug like in the case of vector vs point. This is important as
# vec*mtx and pnt*mtx have a different meaning and only differ in the
# (in Maya non existant) w component of a vector attribute
_NUM = "f"
_VEC = "v"
_PNT = "p"
_MTX = "m"
_CRV = "crv"
_SRF = "srf"
_TYPE = rf"(?:{_NUM}|{_VEC}|{_PNT}|{_MTX}|{_CRV}|{_SRF})"
# _REPLACE allows for f-string like syntax in attributes
# which gets resolved during execution by the parser:
# v@{node}.translate
_REPLACE = r"(?:{[A-Za-z_][A-Za-z_0-9]*})"
_NAME = rf"(?:{VARIABLE}|{_REPLACE})+"
ATTRIBUTE = rf"(?:{_TYPE}@{_NAME}(?:\.{_NAME}(?:\[\d+\])?)+)"
# now that we have numeric values, variables, functions, vectors and
# attributes, we can combine it all to a single expression
# if you want to implement this yourself, pay attention to the order
# a variable and a function will both match against the variable
# pattern but only the function will give you the full token
ATOM = rf"(?:{FUNC}|{VAR}|{VEC_ACCESS}|{VEC}|{NUMERIC}|{ATTR})"My initial plan was to define all possible expressions as regex as well and use groups to extract the important parts. Given how nested some of these expressions are and how regex numbers groups, this proved to be far more messy and complicated than anticipated. Fortunately, this isn't needed! The next step is about extracting this information from expressions.
In this version, the separator token for expressions is the newline character. To prevent the parser from ripping apart brackets stretching across multiple lines, I had to clean them up first:
def compress_multi_line_brackets(text, brackets="()[]"):
# add a quick check if our text overall is valid
if not brackets_are_valid(text, brackets):
raise ExprSyntaxError("Found unmatched or unbalanced brackets")
lines_new = []
lines_old = text.split("\n")
i = 0
while i < len(lines_old):
lines_new.append(lines_old[i])
# while the current line isnt valid, add the next
while not brackets_are_valid(lines_new[-1], brackets):
i += 1
lines_new[-1] += lines_old[i]
i += 1
return "\n".join(lines_new)Splitting the code now at newline characters yields a list of expressions. Extracting tokes turns out to be pretty simple as well. All that is needed is to match the current line against the atom and operator pattern. If found, remove that part from the line and repeat the process.
# get a list of expressions, skip empty lines
expressions = [l.strip() for l in text.split("\n") if l.strip()]
self._lines = []
for expr in expressions:
self._lines.append([])
while expr:
# match against the atom expression
match = ATOM.match(expr)
# if there is no match, match it against the operators
if not match:
match = PATTERN.OPERATOR.match(expr)
# if there is still no match, throw an error
if not match:
raise ExprSyntaxError(expr)
# create a token from the match and add it to the line
# token is for convenience and gets and stores the atom type
self._lines[-1].append(Token.Token(match[0]))
# remove the token from the expression and strip spaces
expr = expr[match.end():].strip() Here is what some tokenized expressions look like at this point. Keep in mind that there is no semantic error checking so far. So "10 = 3" is perfectly fine to tokenize.
"x + 5.0" -> [var{x}, op{+}, [num{5.0}]
"y = 10" -> [var{y}, op{=}, [num{10}]
"c = sqrt(a^2+b^2)" -> [var{c}, op{=}, func{sqrt(a^2+b^2)}]
"2 * (b+c)" [num{2}, op{*}, op{(}, var{b}, op{+}, var{c}, op{)}]With this, I was able to start the interpretation process. The fun part (or so I thought)! The expressions I wanted to support were the:
assignment (=)
logical (&&, ||)
comparison (==, !=, >, >=, <, <=)
line* (+, -)
point* (*, /)
power (^)
atom (an atom by itself is also a valid expression)
*German math students learn ":" instead of "/" as a division operator so mult/div ops are called "point ops" and add/sub "line ops"
I listed them in order of evaluation already. Basically, the closer to the bottom, the higher the precedence of the operation (or simply, the stronger the glue that binds the operands together). Don's implementation for this is fairly easy, yet I struggled to visualize it and I have a hard time putting it in words here as well. Simply, evaluate the atom first, then check if there is a power op, if so, evaluate that, regardless if there was one or not, check if there is a point op, if so evaluate that, regardless if there was one or not, check if there is a line op, ... and so on. In code, this looks reversed. This basically builds and parses an AST at the same time.
def eval_assignment(self):
expr = self.eval_logical()
# if the next token is not part of the assignment ops,
# there is no need to do anything related to assignments
while self.next_token_matches(Operators.ASSIGNMENT):
operator = self.next_token()
expr_right = self.eval_logical()
# even in the case this being an expression, the expr var that
# gets returned is not reassigned so "x=(y=z=2+3)+4" is valid
# and assigns y=5, z=5, x=9. While eval_assignment() itself is
# not recursive, eval_atom() calls it again if it encounters
# an open bracket that does not belong to a function
# I will explain self.lib() below
Expressions.assignment(expr, expr_right, operator, self.lib())
return expr
def eval_logical(self):
expr = self.eval_comparison()
# if the next token is not part of the logical ops, there is no
# need to do anything related to logical operations
while self.next_token_matches(Operators.LOGIC):
operator = self.next_token()
expr_right = self.eval_comparison()
expr = Expressions.universal_logic(expr, expr_right, operator)
return
def eval_comparison(self):
# this is really now just the same as eval_logical() but with
# Operators.COMPARE and Expressions.universal_compare()
...
def eval_power(self):
# same as above with one added step. If the first token is a minus
# operator, then set:
# `expr = Expressions.universal_math(expr, -1, "*")`
# this means that `-5^2 == 25` as in my implementation the
# unary operator{-} has a higher precedence as the power operator
# this is different than in python where `-5^2 == -25`
...
def eval_atom(self):
# this is again where a lot of the heavy lifting happens and I will
# shorten it for the sake of this post
token = self.next_token()
# if we have an open bracket, evaluate from the top down again
if token.type() == TYPE.BRACKET_OPEN:
expr = self.eval_assignment()
if self.next_token_type() != TYPE.BRACKET_CLOSE:
raise ExprSyntaxError("Missing ')'")
return expr
# check if we have a function, here, function calls with multiple
# arguments are not supported as arguments as the arg splitting is
# too primitive. so sin(cos(x)) is valid, so is foo(bar(x), x)
# but foo(bar(x,y)) is not
# you might notice the eval() method and its lib argument, I will
# get to that below
if token.type() == TYPE.FUNCTION:
name = token.split("(")[0]
args = token.partition("(")[2][:-1].split(",")
args = [ExpressionParser(arg).eval(self.lib()) for arg in args]
return Expressions.function(name, args, self.lib())
# numeric constants
if token.type() == TYPE.NUMERIC:
return Expression.number(token)
# attribute
if token.type() == TYPE.ATTRIBUTE:
return Expressions.attribute(token)
# variables, vectors, access, etc
...Two new things in here. First, the Expressions.*, second, the ExpressionParser.eval() and self.lib() functions.
self.lib()
As there are variables and multiple expressions in play, as well as functions, I needed a way to keep track of all of that. self.lib() is a dict containing all functions and variables. It's also used to replace the {name} placeholders in attributes. ExpressionParser.eval() is just a simple wrapper that updates the library with whatever the user wants to pass in. By default, lib contains a couple of standard functions:
IF(condition, if_true, if_false): pretty self-explanatory I think^^
STATIC(attr): this takes an attribute, calls cmds.getAttr() and creates a float constants/colorConstants/fourByFourMatrix node, and returns a new attribute pointing at that
ABS(value): absolute value, returns magnitude for vectors
SIN/COS/TAN(value): trig functions
NORMALIZE(value): normalize vectors
SQRT(value): square root
BLEND(value_a, value_b, factor): lerp, does not support matrices
EVAL(crv, value_u): evaluates the position on a curve at u
EVAL(surface, value_u, value_v): evaluates the position on a surface at (u,v)
REVERSE(curve): reverses the direction
REVERSE(surface, mode): reverses the direction on the surface based on mode. Supported are: 0-u, 1-v, 2-u&v
REBUILD(curve, spans_u): rebuild curve
REBUILD(surface, spans_u, spans_v): rebuild a surface
CLOSEST_POINT(curve/surface, position): returns the closest point on a curve/surface
CLOSEST_PARM(curve, position): returns the closest u parameter as float attribute
CLOSEST_PARM(surface, position): returns the closest u and v parameters as vec3 attr with the z value as 0
ISDEF(variable): returns if a variable is defined
BUILD_MATRIX(aim, up, side, pos): return a matrix attribute, vectors are taken as they are and put into x, y, z, and w rows of the matrix. The 4th column is [0,0,0,1] regardless of the input.
Most, not all of these functions are sensitive to the input they get. If a constant value like -5 is passed into the ABS() function, a numeric expression of 5 gets returned. If an attribute gets passed in, an attribute containing the result of the operation gets returned. Unless STATIC() was called, these nodes are all still connected and will respond to changes in the attribute values.
Expressions.*
The expression functions handle the actual interpretation. There is also quite a bit of decision-making going on based on types. As this is also a lengthy one, I am just gonna use the universal math function as an example:
def _add_float_float(a, b):
return number(str(a + b))
...
def _add_float_vec(a, vb):
return vector(str([a + vb[0], a + vb[1], a + vb[2]]))
...
def _add_attrFloat_attrFloat(a, b):
fm = cmds.createNode("floatMath")
cmds.connectAttr(a, f"{fm}.floatA")
cmds.connectAttr(b, f"{fm}.floatB")
return attribute(f"f@{fm}.outFloat")
...
MATH_LUT = {
("+", "float", "float") : _add_float_float,
("+", "float", "vec") : _add_float_vec,
("+", "attrFloat", "attrFloat"): _add_attrFloat_attrFloat,
...
}
def universal_math(left, right, operator):
if left.is_attribute() or right.is_attribute():
left = left.build_attribute()
right = right.build_attribute()
key = (operator, left.exact_type(), right.exact_type())
if key not in MATH_LUT:
err = f"{left.exact_type()}{operator}{right.exact_type()}"
raise ExprArithmeticError(f"Undefined operation: {err}")
return MATH_LUT[sa_key](left.evaluate(), right.evaluate())Essentially there are a lot of small utility functions that handle each atomic interaction. A nice side effect of this is that certain parts of expression automatically get simplified. Take attr*(3+2). 3+2 evaluates to a number(5). So 5 gets put into its own attribute, not 3 and 2 both.
Conclusion
So what can this thing do now? What are the limitations?
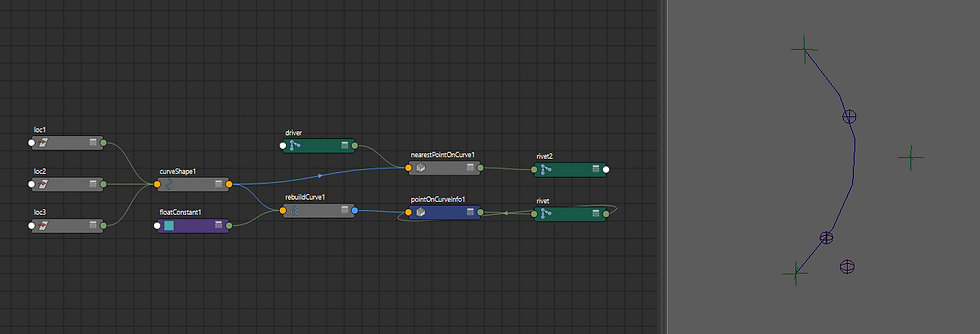
Given the expression:
v@curve.cv[0] = v@loc1.t
v@curve.cv[1] = v@loc2.t
v@curve.cv[2] = v@loc3.t
v@rivet.t = EVAL(REBUILD(crv@curve.ws[0], 5), f@rivet.parameter)
v@rivet2.t = CLOSEST_POINT(crv@curve.ws[0], v@driver.t)
f@rivet.parameter = 0.3And the Python script:
cmds.file(new=True, force=True)
cmds.spaceLocator(name='loc1')
cmds.spaceLocator(name='loc2')
cmds.spaceLocator(name='loc3')
cmds.createNode('joint', name='driver')
cmds.createNode('joint', name='rivet')
cmds.createNode('joint', name='rivet2')
cmds.curve(name='curve', p=[[0,0,0], [0,0,0], [0,0,0]], d=2)
cmds.setAttr('loc1.t', 2, 20, 1)
cmds.setAttr('loc2.t', 10, 12, 1)
cmds.setAttr('loc3.t', 1, 3, 2)
cmds.setAttr('driver.t', 5, 5, 5)
parser = ExpressionParser.from_file("rivets.mx")
parser.eval()This creates node networks for two rivets. On the first, it adds a parameter attribute and attaches it to a reparameterized version of the curve. The second rivet is attached to the closest position on the curve from the driver node.
(It also connects the 3 locators to the curve but that's boring^^)
Another, more complex example that shows some limitations. Here I implemented the parallel transport algorithm:
cmds.file(new=True, force=True)
# create a curve and locators
num_locs = 5
cmds.curve(name="curve", p=num_locs * [[0, 0, 0]], d=2)
locs = [cmds.spaceLocator(name="loc0")[0] for i in range(num_locs)]
# connect the locators to the curve in a loop
# not really very useful, but I had to start somewhere
# the shortened regex patterns above dont show the replacement for the
# index that I am using here, keep that in mind
# this also spreads out the locators on the x axis
for i, node in enumerate(locs):
expr = """
v@curve.cv[{idx}] = v@{node}.t
v@{node}.t = idx * [5,0,0]
"""
ExpressionParser(expr).eval({"node": node, "idx": i})
# rebuild the curve
parser = ExpressionParser("crv = REBUILD(crv@curve.ws[0], 5)")
parser.evaluate()
crv = parser.lib()["crv"]
# create rivets on the curve
num_rivets = 10
up = [0, 1, 0]
DEBUG = False
for i in range(num_rivets):
# to get a proper aim vector, the last sits at 0.999 instead of 1
# this is just me being lazy for this test, implement it properly
# in your project
parm = min(i / (num_rivets-1), 0.999)
# create the joint, calculate matrix and set debug attributes
node = cmds.createNode("joint")
expr = """
pos = EVAL(crv, parm)
pos_aim = EVAL(crv, parm+0.001)
aim = NORMALIZE(pos_aim-pos)
side = NORMALIZE(aim ^ up)
up = NORMALIZE(side ^ aim)
m@{node}.opm = BUILD_MATRIX(aim, up, side, pos)
f@{node}.displayLocalAxis = DEBUG
f@{node}.radius = IF(DEBUG, 0.5, 1)
"""
parser = ExpressionParser(expr)
parser.evaluate({
"up": up,
"node": node,
"parm": parm,
"crv": crv,
"DEBUG": DEBUG
})
up = parser.lib()["up"]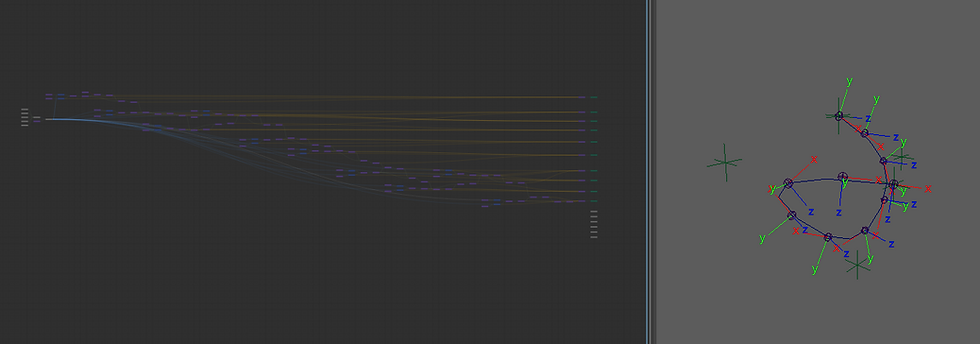
It works, but it's quite messy... The biggest limitation at this point seemed to be missing flow control. While there is the basic IF() function, this was more shoehorned into it after the fact. I did not think about integrating conditions or loops before. The IF() was fairly easy, but the for loop would be a lot trickier with the current architecture.
The second big caveat was the underlying code itself. While I based mine on Don's post, our project scopes and goals were quite different. This meant not all decisions were as suitable for my use case as they were for his and at times hindered the development of new features.
The third issue, and possibly just another excuse to make this more complicated, was that so far, nothing was properly typed. I spare you my thoughts on dynamically typed languages (yes, my beloved Python included), but generally, I prefer statically typed. This would also allow me to introduce new types more easily even if they had no Maya attribute equivalent but could instead be used for static computations. Eg mtx3, vec2, vec4, etc.
With that, I had some new requirements for my next version... More on that shortly :)
Cheers!







Comments